Overview
The Divide-n-Conquer strategy often employs recursion, as it relies on applying the same method to reduce the problem size by half and subsequently combining the outcomes for the ultimate solution.
I view Divide-n-Conquer in a light similar to MapReduce, particularly when the task involves transformation. MapReduce breaks down a large problem into more manageable, independent sub-problems. Since each of these sub-problems operates autonomously, we can address them sequentially and still integrate their solutions. Key to this approach is ensuring the main problem can be independently segmented and the derived solutions can be seamlessly merged.
The typical blueprint for Divide-n-Conquer involves a recursive function. This function produces a result when the size becomes null and provides mechanisms to split the problem and amalgamate the solutions. Consequently, time complexity predominantly depends on this recursive function.
Example Questions
108. Convert Sorted Array to Binary Search Tree
Given an integer array `nums` where the elements are sorted in **ascending order**, convert _it to a_
**_height-balanced_**
_binary search tree_.
**Example 1:**
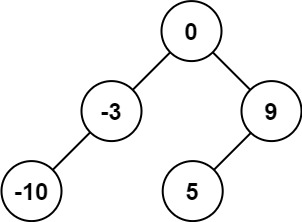
**Input:** nums = [-10,-3,0,5,9]
**Output:** [0,-3,9,-10,null,5]
**Explanation:** [0,-10,5,null,-3,null,9] is also accepted:

**Example 2:**
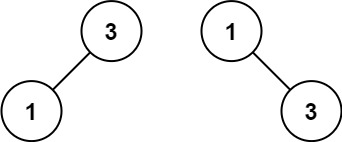
**Input:** nums = [1,3]
**Output:** [3,1]
**Explanation:** [1,null,3] and [3,1] are both height-balanced BSTs.
Solution:
The question asks to transform the sorted array into a height-balanced BST so:
- the number of nodes on the left and right should be very close -> implies how to divide the question
- the BST is resulted from the sorted array -> indicates transformation
- If we split the array into separate arrays, each array is still sorted and can be transformed into a height-balanced BST, thus we can make a BST using these small BST
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
# We need an recursion to convert the divided arrays into BST
def helper(nums):
# if the array is empty, we should create a null node
if len(nums) == 0:
return None
# if there is only one value in the array, this tree has only one node
if len(nums) == 1:
return TreeNode(nums[0])
# we are building a height-balanced BST, thus we should divide the nums array into half each time
mid = len(nums) // 2
# the value at the mid is the root
root = TreeNode(nums[mid])
# the left branch is the BST resulted from the left half array
root.left = helper(nums[:mid])
# the right branch is the BST resulted from the right half array
root.right = helper(nums[mid+1:])
return root
return helper(nums)
Time Complexity: O(N) even it is recursion, we are visiting each element exactly once
Space Complexity: O(logN) it is the height of the BST tree we are creating
215. Kth Largest Element in an Array
Given an integer array `nums` and an integer `k`, return _the_ `kth` _largest element in the array_.
Note that it is the `kth` largest element in the sorted order, not the `kth` distinct element.
Can you solve it without sorting?
**Example 1:**
**Input:** nums = [3,2,1,5,6,4], k = 2
**Output:** 5
**Example 2:**
**Input:** nums = [3,2,3,1,2,4,5,5,6], k = 4
**Output:** 4
**Constraints:**
- `1 <= k <= nums.length <= 105`
- `-104 <= nums[i] <= 104`
Solution
This solution is to use quick select to find the Kth largest value from a non-sorted array. Quick select is essentially divide-n-conquer as:
- we divide the array using a random pivot
- check which subarray could contain the
kthlargest value - continue the search until we get the result
- we need a
recursionfunction to work on each array
import heapq
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
def quick_select(nums, k):
# random select a value from the array
pivot = random.choice(nums)
# create the subarray contains the larger, smaller and equaivalent values
more, less, equal = [], [], []
for num in nums:
if num > pivot:
more.append(num)
elif num < pivot:
less.append(num)
else:
equal.append(num)
# If there are more than k elements larger than the pivot in array more, we can search kth largest value from more and it is same kth largest value as the original array
if len(more) >= k:
return quick_select(more, k)
# If the number of larger and equaivalent values are less than k, the kth largest value should be in less array, but we cannot find kth largest value from less since it will result in a much smaller value.
# we need identify the new kth target in the less array
if len(more) + len(equal) < k:
return quick_select(less, k - len(more) - len(equal))
# otherwise, the pivot should be the kth largest value
return pivot
return quick_select(nums, k)
23. Merge k Sorted Lists
You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
_Merge all the linked-lists into one sorted linked-list and return it._
**Example 1:**
**Input:** lists = [[1,4,5],[1,3,4],[2,6]]
**Output:** [1,1,2,3,4,4,5,6]
**Explanation:** The linked-lists are:
[
1->4->5,
1->3->4,
2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6
**Example 2:**
**Input:** lists = []
**Output:** []
**Example 3:**
**Input:** lists = [[]]
**Output:** []
**Constraints:**
- `k == lists.length`
- `0 <= k <= 104`
- `0 <= lists[i].length <= 500`
- `-104 <= lists[i][j] <= 104`
- `lists[i]` is sorted in **ascending order**.
- The sum of `lists[i].length` will not exceed `104`.
Solution
This is an advanced question based off 21. Merge Two Sorted Lists.
And this question has the following characteristics leading to divide-n-conquer:
- merge k sorted list is the same as merge 2 sorted lists, since we want one single sorted list in the end
- it is similar to MapReduce, aggregate multiple lists into one list
- the merge of any two lists doesn’t affect the final result nor the merge of any other lists
Thus, we could divide the list of k sorted lists into several lists and each contains 1 or 2 sorted lists for us to merge. Then we can always merge 2 sorted lists.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
# merge 2 sorted lists recursively
def merge2list(list1, list2):
if not list1:
return list2
if not list2:
return list1
# Choose the smaller head node and merge the remaining nodes.
if list1.val > list2.val:
new_node = ListNode(list2.val)
new_node.next = merge2list(list1, list2.next)
else:
new_node = ListNode(list1.val)
new_node.next = merge2list(list1.next, list2)
return new_node
n = len(lists)
# Base cases: empty or single list.
if n == 0: return None
if n == 1: return lists[0]
# Split lists in half and merge recursively.
left_merged_lists = self.mergeKLists(lists[:n//2])
right_merged_lists = self.mergeKLists(lists[n//2:])
# Merge the two halves.
return merge2list(left_merged_lists, right_merged_lists)
Time Complexity: O(NlogK) where N is the number of total elements in lists, since we divide lists into half so the height of the resulted tree is logK, and each node need to visit all elements waiting to be sorted thus the actual time should be $O(∑_{i=1}^N logk)=O(Nlogk)$
Space Complexity: O(NlogK) the height of recursion stack should logK for mergeKLists and merge2list could need N stacks in the worst case (the recursion stack could go up to N)
Takeaways
When faced with unknown data in a query that requires consolidation into a single data point, and where partial data aggregation won't affect the overall outcome or aggregation of other data, it's advisable to employ the `divide-n-conquer` approach. This strategy is particularly relevant if the scenario reminds you of MapReduce.